Science:Mathmatics

Mathematics

Caption	Lebombo Bone
Name	Mathematics
Type	Formal
Origin	Africa

Summary

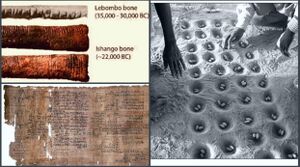
The origins of mathematics trace back to ancient Africa, particularly Egypt and Mesopotamia, where early civilizations developed arithmetic, geometry, and basic algebra. Around 3000 BCE, the Egyptians used mathematics for building, astronomy, and record-keeping, creating one of the earliest base-10 counting systems. The Ishango bone, discovered in the Congo, dates back to around 20,000 BCE and is believed to be one of the oldest mathematical artifacts, showcasing early counting or tallying. These African contributions laid foundational principles that influenced later mathematical development in other regions.

Caption	Lebombo Bone
Name	Mathematics
Type	Formal
Origin	Africa

History

The Lebombo bone from the mountains between Swaziland and South Africa may be the oldest known mathematical artifact.[38] It dates from 35,000 BCE and consists of 29 distinct notches that were deliberately cut into a baboon's fibula.[39][40]

The Ishango bone is a bone tool from the Democratic Republic of Congo dated to the Upper Paleolithic era, about 18,000 to 20,000 BCE. It is also a baboon's fibula,[41] with a sharp piece of quartz affixed to one end, perhaps for engraving or writing. It was first thought to be a tally stick, as it has a series of tally marks carved in three columns running the length of the tool, but some scientists have suggested that the groupings of notches indicate a mathematical understanding that goes beyond counting. Various functions for the bone have been proposed: it may have been a tool for multiplication, division, and simple mathematical calculation, a six-month lunar calendar,[42] or it may have been made by a woman keeping track of her menstrual cycle.[43]

The Bushong people can distinguish graphs that have Eulerian paths and those that do not. They use such graphs for purposes including embroidery or political prestige.

Northern Africa and the Nile Valley

By the predynastic Naqada period in Egypt, people had fully developed a numeral system.[citation needed] The importance of mathematics to an educated Egyptian is suggested by a New Kingdom fictional letter in which the writer proposes a scholarly competition between himself and another scribe regarding everyday calculation tasks such as accounting of land, labor and grain.[53] Texts such as the Rhind Mathematical Papyrus and the Moscow Mathematical Papyrus show that the ancient Egyptians could perform the four basic mathematical operations—addition, subtraction, multiplication, and division—use fractions,[54] knew the formula to compute the volume of a frustum, and calculate the surface areas of triangles, circles and even hemispheres.[55] They understood basic concepts of algebra and geometry, and could solve simple sets of simultaneous equations.

Mathematical notation was decimal, and based on hieroglyphic signs for each power of ten up to one million. Each of these could be written as many times as necessary to add up to the desired number; so to write the number eighty or eight hundred, the symbol for ten or one hundred was written eight times respectively.[57] Because their methods of calculation could not handle most fractions with a numerator greater than one, ancient Egyptian fractions had to be written as the sum of several fractions. For example, the fraction two-fifths was resolved into the sum of one-third + one-fifteenth; this was facilitated by standard tables of values.[58] Some common fractions, however, were written with a special glyph; the equivalent of the modern two-thirds is shown on the right.[59]

Ancient Egyptian mathematicians had a grasp of the principles underlying the Pythagorean theorem, knowing, for example, that a triangle had a right angle opposite the hypotenuse when its sides were in a 3–4–5 ratio.[60] They were able to estimate the area of a circle by subtracting one-ninth from its diameter and squaring the result:

Area ≈ [(8⁄9)D]2 = (256⁄81)r2 ≈ 3.16r2, a reasonable approximation of the formula πr2.[60][citation needed]

The golden ratio seems to be reflected in many Egyptian constructions, including the pyramids, but its use may have been an unintended consequence of the ancient Egyptian practice of combining the use of knotted ropes with an intuitive sense of proportion and harmony.[61]

Based on engraved plans of Meroitic King Amanikhabali's pyramids, Nubians had a sophisticated understanding of mathematics and an appreciation of the harmonic ratio. The engraved plans is indicative of much to be revealed about Nubian mathematics

Principles

The main principles of mathematics are foundational concepts that underpin the discipline and guide mathematical reasoning. These include:

Numbers and Arithmetic: Understanding different types of numbers (e.g., integers, fractions, real numbers) and operations (addition, subtraction, multiplication, division).

Algebra: Using symbols and rules to represent and solve equations and analyze relationships between quantities.

Geometry: Studying shapes, sizes, properties of space, and the relationships of points, lines, and surfaces.

Logic and Proof: Applying formal reasoning and structured arguments to verify truths, form hypotheses, and construct proofs.

Calculus: Examining change and motion through concepts like limits, derivatives, and integrals, crucial for advanced analysis.

Statistics and Probability: Analyzing data and understanding likelihood and patterns to make informed predictions and decisions.

Key Developments

Mathematics has led to numerous key developments that have transformed science, technology, and everyday life. Some notable advancements include:

The Development of Calculus: By Newton and Leibniz in the 17th century, calculus revolutionized physics, engineering, and economics by enabling precise analysis of change and motion.

Statistics and Probability Theory: These provided methods to analyze data, make predictions, and informed decision-making, impacting fields like medicine, social sciences, and finance.

Algebra and Algebraic Structures: Advanced algebra facilitated the understanding of complex systems and laid the groundwork for modern cryptography, crucial for data security.

Number Theory: This area of study, foundational to cryptography, enables secure online transactions, impacting e-commerce and communication.

Geometry and Trigonometry: Essential for architecture, navigation, astronomy, and even computer graphics, shaping both practical applications and theoretical exploration.

Set Theory and Logic: Foundational to computer science and theoretical mathematics, enabling programming languages, algorithms, and artificial intelligence.

Complex and Imaginary Numbers: These expanded our ability to solve equations beyond real numbers, critical in electrical engineering, quantum mechanics, and signal processing.

Applications

Mathematics has numerous key applications across diverse fields, enabling advancements, innovations, and everyday functions. Some of these applications include:

Engineering: Mathematics is essential for designing structures, analyzing materials, and solving complex problems in electrical, mechanical, and civil engineering.

Physics and Astronomy: Mathematical models and equations describe physical laws, predict planetary motion, and facilitate discoveries in space exploration.

Computer Science: Algorithms, cryptography, and data structures rely on mathematical principles for programming, data security, and artificial intelligence development.

Economics and Finance: Mathematics underpins models for pricing, risk assessment, investment strategies, and economic forecasting, crucial for decision-making in finance.

Medicine and Biology: Statistics and calculus are used in medical imaging, genetic research, disease modeling, and drug development to analyze data and improve health outcomes.

Environmental Science: Mathematics aids in modeling climate patterns, studying ecosystems, and managing resources for sustainability.

Data Science and Machine Learning: Mathematical techniques in statistics, linear algebra, and calculus enable data analysis, predictive modeling, and training of AI systems.

Architecture and Art: Geometry and symmetry are used to design buildings, create visual art, and establish aesthetic principles.

These applications highlight mathematics as a versatile and vital tool across all areas of life and science.